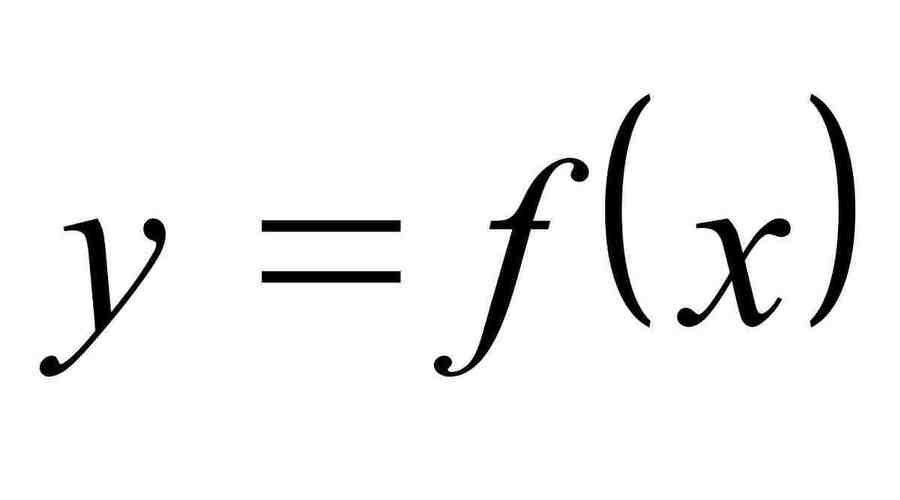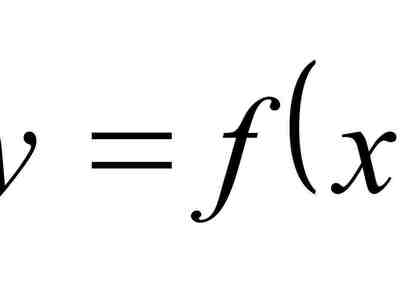Зачем нужны эти производные?
В школе на математике мы изучаем производные, логарифмы, тригонометрию, интегралы и прочее. Но зачем это надо? Пригодится ли это в жизни? На эти вопросы учителя обычно не могут ответить...
Когда-то в школе я не понимал производных. Не подумайте, что я был совсем уж дураком — я знал определение, умел их брать (в рамках простеньких школьных примеров) и оценки по математике имел неплохие.
Но вот смысл этого понятия от меня ускользал. Я понимал насколько важен график некоторой функции — по нему легком можно увидеть зависимость функции от аргумента. Глянул в какую-нибудь точку — и сразу ясно положение дел в данном конкретном месте. И что с этого?
Смысл производной
Смысл производной
Ну вот почему я не увидел этот ролик лет так ...дцать назад? Чтобы заинтересовать уроком, в своё время, нужно всего лишь было объяснить и показать пару примеров!
Сложность подачи информации о производной заключается в том, что это одно из абстрактных понятий, физический смысл которых трудно представить наглядно. Если, например, численные величины, их сумму и произведение, возведение в степень несложно объяснить в понятиях окружающего мира (количество, площадь, объем и т.п.), то смысл производной зачастую ускользает от понимания школьников, поэтому они могут выполнять задачи на ее вычисление чисто механически по затверженным формулам.
Это ведет к тому, что в процессе решения учащийся не сможет справиться с заданиями, хоть немного отличающимися от шаблонных, и с такими неравенствами и системами уравнений, где надо применить навыки математического мышления.
Производная, как известно, характеризует скорость изменения функции в конкретной точке. Определение этого понятия звучит достаточно сложно:
«предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует».
Трудность понимания этого определения с точки зрения школьника можно охарактеризовать как «все слова по отдельности понятны, а общий смысл уловить не получается». Разумеется, без подробного и наглядного объяснения ученику останется лишь затучить эту фразу, не понимая ее смысла.
Как же понять смысл производной? Ниже -, простой пример из повседневной жизни.
Допустим, два ученика одного класса — назовем их Иванов и Петров — получили за контрольную работу по теме «Системы уравнений и неравенств» по оценке «четыре». При этом Иванов весьма доволен, а Петров опечален. Такое их отношение к оценке станет понятным, если мы будем знать, что Петров — круглый отличник, а Иванов ни разу не получал по математике выше «тройки».
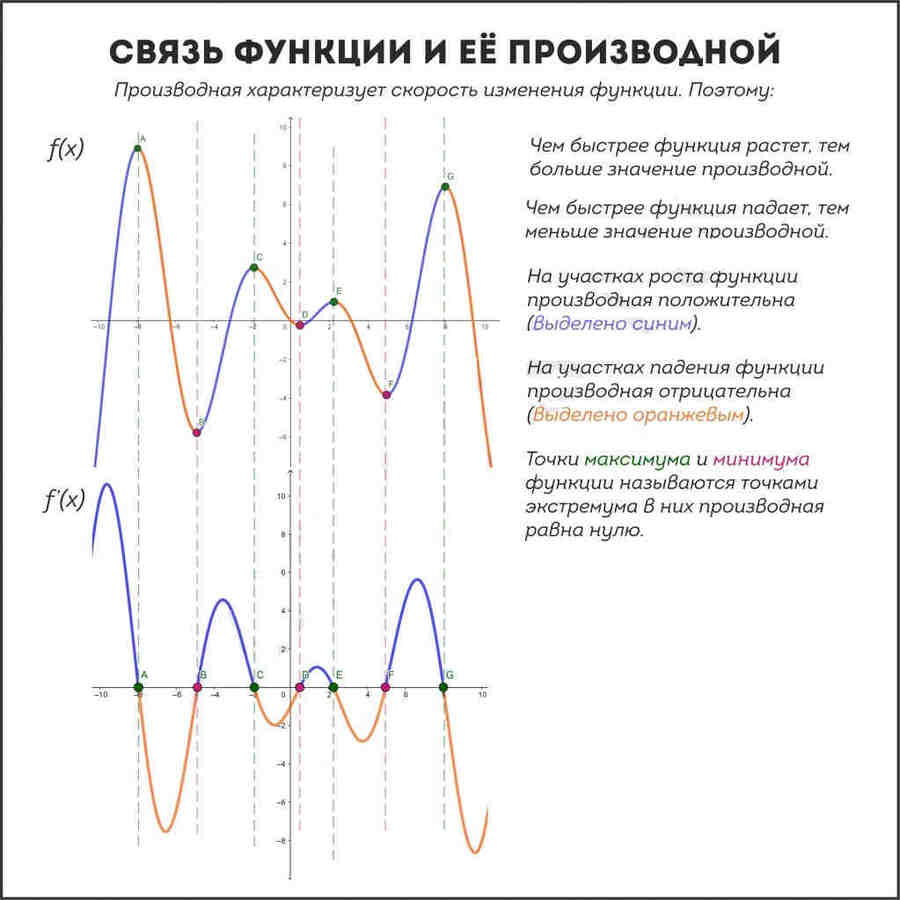
То есть, если рассматривать их оценки в динамике, мы видим, что у Иванова наблюдается прирост успеваемости (функция растет, ее производная положительна), а у Петрова, напротив, падение (функция убывает, производная отрицательна). То есть конкретная оценка (точка на графике функции) отображает текущее положение дел, а производная (касательная к графику в этой функции) показывает нам тенденцию развития ситуации.
![Физический смысл производной]()
Физический смысл производной
Аналогично в физике: движение тел характеризуется не только скоростью, но и ускорением, то есть тем, увеличивается или уменьшается ли его скорость. На этих или других подобных примерах можно пояснить, что производная — важнейшая характеристика именно динамики любых процессов, то есть она описывает закон, по которому изменяется мгновенное значение любой функции.
И чтобы вообще добить...
А что такое производная от производной?
Если мы берем какую-то физическую величину, и берем от нее производную, например, от времени, это означает скорость возрастания этой физической величины от времени. Простой пример: берем расстояние, которое прошел человек, выражаем ее какой-то формулой, берем производную от этой формулы по времени, получаем- угадайте что? Скорость этого человека! Но, очень важно упомянуть, что мы получаем скорость этого человека от времени.
Круто! Значит, если мы возьмем производную от скорости по времени, то мы получим скорость возрастания... Скорости? Ну, да, как-то так.
Лично я всегда понимал все гораздо проще на примерах, поэтому:
Идет человек ранним утром, и пьет кофе. Каждый раз, когда он выпивает глоток, то его скорость увеличивается, но увеличивается постепенно. Значит, его скорость растет, значит человек ускоряется.
Итак, в общем случае, физический смысл производной- скорость роста той или иной величины в зависимости от той величины, по которой мы берем эту самую производную. Если мы возьмем производную еще раз, получим скорость возрастания скорости и так далее. Все просто (наверное)
Теги к статье
Поделиться статьёй и ссылки
Комментарии
Вы должны авторизоваться, чтобы оставлять комментарии.