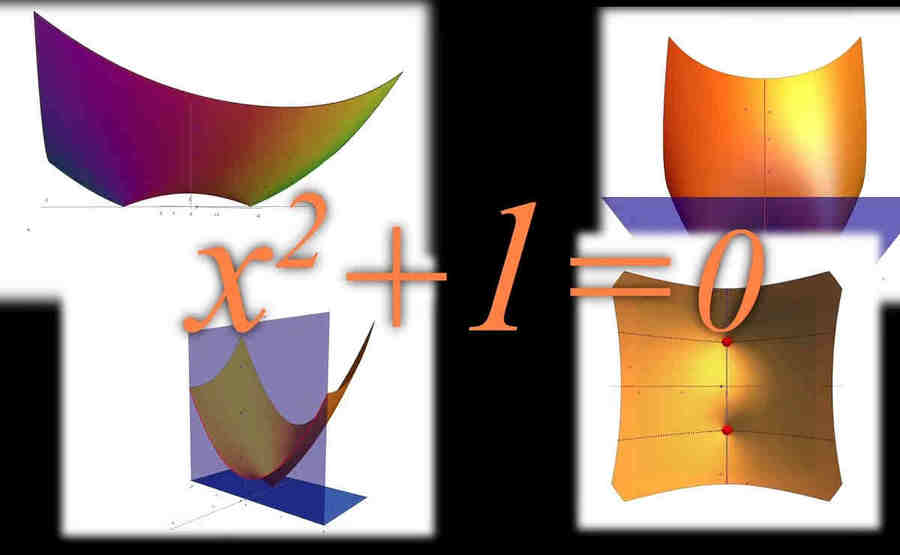Мнимые числа

Часть 1. Откуда и зачем?

Часть 2

В прошлом видео ребята из Welch Labs упомянули, как долго и трудно математические инновации внедрялись в общественное сознание. Теперь мы перенесемся в Италию времён Ренессанса. Удивительное время: эти люди боялись и избегали отрицательных чисел, но при этом выводили такие формулы, что современные школьники падают в ужасе, и даже студенты нервничают. Одна из таких формул привела к появлению мнимых чисел. 

Часть 3

Из этого видео от Welch Labs вы узнаете, как Рафаэль Бомбелли, ученик мастера математических дуэлей, Джеролама Кардано, прошёл трудный путь от отрицания мнимых чисел до их принятия. По крайней мере, частичного: Бомбелли допустил, что числа с нужными ему свойствами могут существовать, и рассчитал, куда они могут его привести. Кстати, как думаете, было ли это открытие, или изобретение?

Часть 4

Из этого видео вы узнаете, как математический дуэлянт Бомбелли закончил дело своего учителя и одолел их общего врага — проблему Кардано. Так началась история мнимых чисел. Даже их отец (или первооткрыватель?) не смог до конца понять, что же перед ним. К счастью, у нас есть огромный багаж послезнания, поэтому давайте в этот раз закончим с историей, а в следующий — начнём разбираться, что же делать с этими числами.

Часть 5

А из этого видео вы узнаете, как с помощью карандаша, листа бумаги и числа i переместиться в другое измерение. Спрашиваете, где взять число i? Не волнуйтесь, все ответы уместились в 4 минуты, и снабжены подробными иллюстрациями.

Часть 6

У вас мог возникнуть вопрос: вот добавили мы к числу ещё одну закорючку, и что дальше? Как это меняет мир? Как помогает решить то уравнение из первого видео? Не переживайте, просто пока у вас нет инструментов для работы с подобными числами. С одним из самых важных мы вас познакомим в этой серии.

Часть 7

Скажем честно: вряд ли кто-то из вас сделал домашнее задание. Канал Welch Labs подготовился к такому развитию событий, и это видео объяснит, что вы должны были сделать и к каким выводам прийти.

Часть 8

Из прошлых выпусков мы знаем два способа представить комплексные числа и два способа, как их делить и умножать. Пора бы уже что-нибудь посчитать, а заодно разобраться, зачем кому-то понадобилось плодить формы записи и без того непонятных чисел.

Часть 9

В математике нельзя просто так взять и ввести новое понятие. Сколь бы не было полезно предложенное нововведение, к нему будут относиться с подозрением, пока вы не предоставите надежного обоснования. Но будьте осторожны, возможно замыкание.

Часть 10

Как бы удручающе это ни звучало, но в нашей повседневности слишком мало пространственных измерений. Возможно, вы никогда не замечали этой проблемы, но физики и математики страдают от неё регулярно. Например, разобраться в комплексных числах было бы гораздо проще, если бы мы могли рисовать четырёхмерные графики. В этом видео вы узнаете, почему это — проблема, а потом обсудим, как её можно решить.

Часть 11

Пора перейти к практике. В этот раз — никаких исторических экскурсов и минимум определений. Просто рисуем линии, преобразуем их, и обсуждаем, что из этого получилось. Самое удивительное, что математики прошлого проделали эту работу почти два века назад, без компьютеров и калькуляторов. Страшно представить, что ещё они могли бы открыть, будь у них современные инструменты.

Часть 12

Что делать, когда ваша задача требует четырёхмерных графиков, а вселенная выдала только три? Ответ очевиден: нужно выдумать что-то новое, непонятное, но при этом обладающие необходимыми вам свойствами. В прошлый раз мы познакомились с многозначными функциями. А из этого видео вы узнаете, зачем.

Часть 13

Наконец, последняя серия. Если вы ждали возможности посмотреть все серии разом за один вечер, то вот она. У многих зрителей ещё после первой возник вопрос: «А что же такое нам, собственно, показали? На самом же деле всё не так!» И вот теперь пришло время расставить все точки над i.